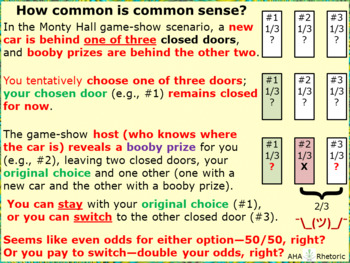
This critical-thinking problem asks you to select 1 of 3 doors to possibly win a prize. After new info, you may then switch your selection. Do you make a quick, gut-level decision, or you do you do the math? This PPT-size animated GIF (5-frame, 4 seconds each, 2 cycles) can be used as a PPT slide that animates when in slide-show mode; it can also be used as a bell-ringer for any class that deals with critical thinking or conditional probability, etc. Image size 960×720 (file size 665 KB). Note 1: You can pause an animated GIF during a PowerPoint Slide Show by Right-Clicking your mouse and then later resume animation with a Left-Click. This mouse-trick works in PPT 2010, but other PPT versions may work differently. Note 2: Alt-text for this image (as in Blackboard with a limit of 100 characters): Prize in 1 of 3 options; pick 1; 1 other revealed as no-prize; stick with 1st pick or pay to switch? Used/tested and engaging with English Composition, English 101. To learn how to make such animated GIFs using PowerPoint and a free online AGIF maker, see PowerPoint slide show Animated-GIFsHow-to-Make-and-Use.

Total Pages

Answer Key

N/A

Teaching Duration

N/A

Report this resource to TPT

Reported resources will be reviewed by our team. Report this resource to let us know if this resource violates TPT’s content guidelines.

Standards

to see state-specific standards (only available in the US).

CCSS7.SP.C.6

Approximate the probability of a chance event by collecting data on the chance process that produces it and observing its long-run relative frequency, and predict the approximate relative frequency given the probability. For example, when rolling a number cube 600 times, predict that a 3 or 6 would be rolled roughly 200 times, but probably not exactly 200 times.

CCSS7.SP.C.7

Develop a probability model and use it to find probabilities of events. Compare probabilities from a model to observed frequencies; if the agreement is not good, explain possible sources of the discrepancy.

CCSS7.SP.C.8

Find probabilities of compound events using organized lists, tables, tree diagrams, and simulation.

Reviews

Questions & Answers

AHA-Rhetoric

See all 46 resources

103 Followers